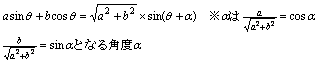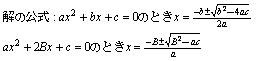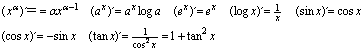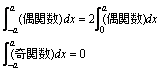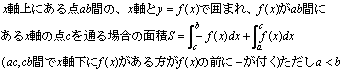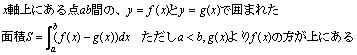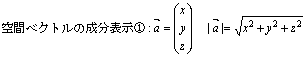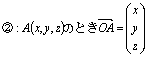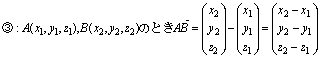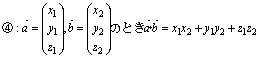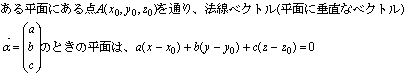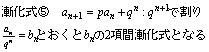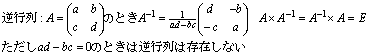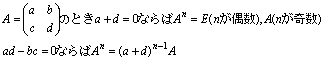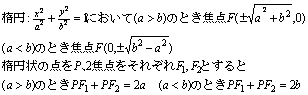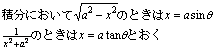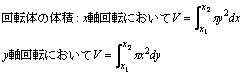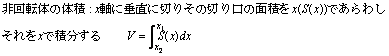数学公式集
|
指数関数 l
l
l
l
l
l
l
l
l
|
注意事項 |
|
対数関数 l
l
l
l
l
l
l
l
l
l
|
・
・真数(公式①での ・①において、 |
|
三角関数 l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
|
|
|
数式処理 l
l
l
l
l
l
l
l
l
|
・因数分解:次数が異なるなら低次の文字で整理 全て同次数なら、1文字整理 ・関数 ・最大公約数:共通な因数の積 最小公倍数:最高次数の因数全ての積 ・恒等式:左辺と右辺の係数を比較 任意の ・ |
|
2次関数等 l
l
l
l
l
l
l
l
l
l
l
l
l
l
|
・2次関数の最大、最小値を求めるときは平方完成を使う |
|
確率 l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
二項定理: l
l
l
l
l
l
l
l
l
l
l
|
|
|
微分(数学Ⅲ) l
l
l
l
l
l
l
l
l
l
l
l
l
|
・ ・ ・
|
|
微積分(数学Ⅱ) l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
|
・方程式 |
|
ベクトル l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
|
|
|
数列 l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
|
|
|
行列 l
l
l
l
l
l
l
l
l
|
|
|
2次曲線 l
l
l
l
l
|
|
|
積分(数学Ⅲ) l
l
l
l
l
l
l
l
l
l
|
|